Kode untuk blog ini, bersama dengan dataset, tersedia di tautan berikut https://github.com/shekharpandey89/k-means
Pengelompokan K-Means adalah algoritme pembelajaran mesin tanpa pengawasan. Jika kita membandingkan algoritma unsupervised clustering K-Means dengan algoritma supervised, maka tidak perlu melatih model dengan data berlabel. Algoritma K-Means digunakan untuk mengklasifikasikan atau mengelompokkan objek yang berbeda berdasarkan atribut atau fiturnya ke dalam sejumlah K grup. Di sini, K adalah bilangan bulat. K-Means menghitung jarak (menggunakan rumus jarak) dan kemudian mencari jarak minimum antara titik data dan cluster centroid untuk mengklasifikasikan data.
Mari kita pahami K-Means menggunakan contoh kecil menggunakan 4 objek, dan setiap objek memiliki 2 atribut.
| Nama Objek | Atribut_X | Atribut_Y |
|---|---|---|
| M1 | 1 | 1 |
| M2 | 2 | 1 |
| M3 | 4 | 3 |
| M4 | 5 | 4 |
K-Means untuk menyelesaikan Contoh Numerik:
Untuk menyelesaikan masalah numerik di atas melalui K-Means, kita harus mengikuti langkah-langkah berikut:
Algoritma K-Means sangat sederhana. Pertama, kita harus memilih sembarang bilangan K dan kemudian memilih centroid atau pusat cluster. Untuk memilih centroid, kita dapat memilih sejumlah objek secara acak untuk inisialisasi (tergantung pada nilai K).
Langkah-langkah dasar algoritma K-Means adalah sebagai berikut:
- Terus berjalan sampai tidak ada objek yang bergerak dari centroidnya (stabil).
- Kami pertama-tama memilih beberapa centroid secara acak.
- Kemudian, kami menentukan jarak antara setiap objek dan centroidsroid.
- Mengelompokkan objek berdasarkan jarak minimum.
Jadi, setiap objek memiliki dua titik sebagai X dan Y, dan mereka mewakili pada ruang grafik sebagai berikut:
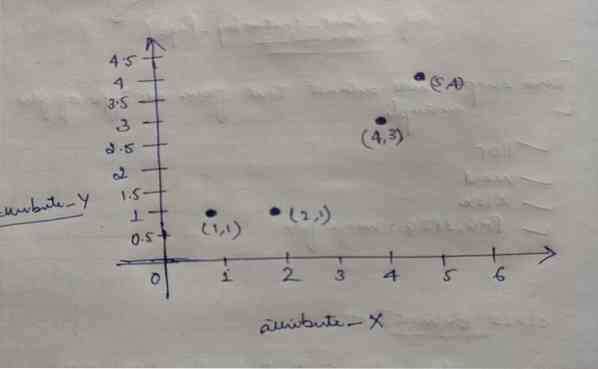
Jadi kami awalnya memilih nilai K=2 secara acak untuk menyelesaikan masalah kami di atas.
Langkah 1: Awalnya, kami memilih dua objek pertama (1, 1) dan (2, 1) sebagai centroid kami. Grafik di bawah ini menunjukkan hal yang sama. Kami menyebutnya centroid ini C1 (1, 1) dan C2 (2,1). Di sini, kita dapat mengatakan C1 adalah grup_1 dan C2 adalah grup_2.
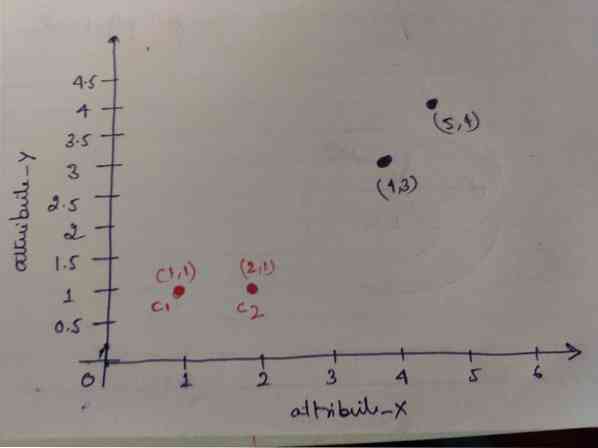
Langkah 2: Sekarang, kita akan menghitung setiap titik data objek ke centroid menggunakan rumus jarak Euclidean.
Untuk menghitung jarak, kami menggunakan rumus berikut:.

Kami menghitung jarak dari objek ke centroid, seperti yang ditunjukkan pada gambar di bawah ini.

Jadi, kami menghitung jarak setiap titik data objek melalui metode jarak di atas, akhirnya mendapatkan matriks jarak seperti yang diberikan di bawah ini:
DM_0 =
| 0 | 1 | 3.61 | 5 | C1 = (1,1) cluster1 | grup 1 |
| 1 | 0 | 2.83 | 4.24 | C2 = (2,1) cluster2 | grup_2 |
| SEBUAH | B | C | D | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | X |
| 1 | 1 | 3 | 4 | kamu |
Sekarang, kami menghitung nilai jarak setiap objek untuk setiap centroid. Misalnya titik objek (1,1) memiliki nilai jarak ke c1 adalah 0 dan c2 adalah 1.
Seperti dari matriks jarak di atas, kita mengetahui bahwa objek (1, 1) memiliki jarak ke cluster1 (c1) adalah 0 dan ke cluster2 (c2) adalah 1. Jadi objek satu dekat dengan cluster1 itu sendiri.
Demikian pula, jika kita memeriksa objek (4, 3), jarak ke cluster1 adalah 3.61 dan ke cluster2 adalah 2.83. Jadi, objek (4, 3) akan bergeser ke cluster2.
Demikian pula, jika Anda memeriksa objek (2, 1), jarak ke cluster1 adalah 1 dan ke cluster2 adalah 0. Jadi, objek ini akan bergeser ke cluster2.
Sekarang, menurut nilai jaraknya, kami mengelompokkan titik-titik (pengelompokan objek).
G_0 =
| SEBUAH | B | C | D | |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | grup 1 |
| 0 | 1 | 1 | 1 | grup_2 |
Sekarang, menurut nilai jaraknya, kami mengelompokkan titik-titik (pengelompokan objek).
Dan terakhir akan terlihat grafik seperti dibawah ini setelah dilakukan clustering (G_0).
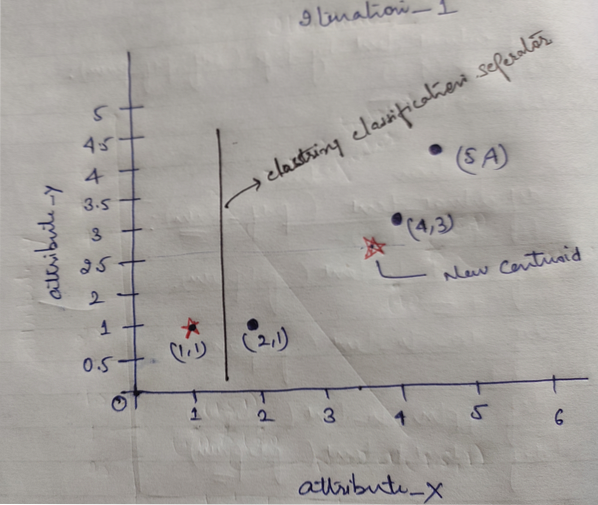
Iterasi_1: Sekarang, kita akan menghitung centroid baru sebagai grup awal yang berubah karena rumus jarak seperti yang ditunjukkan pada G_0. Jadi, grup_1 hanya memiliki satu objek, jadi nilainya masih c1 (1,1), tetapi grup_2 memiliki 3 objek, jadi nilai centroid barunya adalah 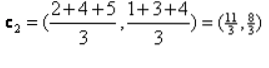
Jadi, c1 baru (1,1) dan c2 (3.66, 2.66)
Sekarang, kita harus menghitung lagi semua jarak ke centroid baru seperti yang kita hitung sebelumnya.
DM_1 =
| 0 | 1 | 3.61 | 5 | C1 = (1,1) cluster1 | grup 1 |
| 3.14 | 2.36 | 0.47 | 1.89 | C2 = (3.66,2.66) cluster2 | grup_2 |
| SEBUAH | B | C | D | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | X |
| 1 | 1 | 3 | 4 | kamu |
Iteration_1 (Pengelompokan objek): Sekarang, atas nama perhitungan matriks jarak baru (DM_1), kami mengelompokkannya sesuai dengan itu. Jadi, kita menggeser objek M2 dari grup_2 ke grup_1 sebagai aturan jarak minimum ke centroid, dan objek lainnya akan sama. Jadi pengelompokan baru akan seperti di bawah ini.
G_1 =
| SEBUAH | B | C | D | |
|---|---|---|---|---|
| 1 | 1 | 0 | 0 | grup 1 |
| 0 | 0 | 1 | 1 | grup_2 |
Sekarang, kita harus menghitung centroid baru lagi, karena kedua objek memiliki dua nilai.
Jadi, centroid baru akan menjadi 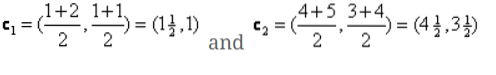
Jadi, setelah kita mendapatkan centroid baru, clusteringnya akan terlihat seperti di bawah ini:
c1 = (1.5, 1)
c2 = (4.5, 3.5)
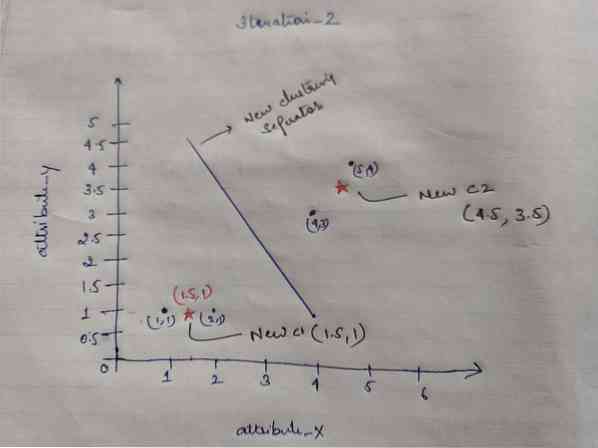
Iterasi_2: Kami mengulangi langkah di mana kami menghitung jarak baru setiap objek ke centroid baru yang dihitung. Jadi, setelah perhitungan, kita akan mendapatkan matriks jarak berikut untuk iterasi_2.
DM_2 =
| 0.5 | 0.5 | 3.20 | 4.61 | C1 = (1.5, 1) cluster1 | grup 1 |
| 4.30 | 3.54 | 0.71 | 0.71 | C2 = (4.5, 3.5) cluster2 | grup_2 |
A B C D
| SEBUAH | B | C | D | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | X |
| 1 | 1 | 3 | 4 | kamu |
Sekali lagi, kami melakukan tugas pengelompokan berdasarkan jarak minimum seperti yang kami lakukan sebelumnya. Jadi setelah melakukan itu, kami mendapatkan matriks pengelompokan yang sama dengan G_1.
G_2 =
| SEBUAH | B | C | D | |
|---|---|---|---|---|
| 1 | 1 | 0 | 0 | grup 1 |
| 0 | 0 | 1 | 1 | grup_2 |
Seperti di sini, G_2 == G_1, jadi tidak diperlukan iterasi lebih lanjut, dan kita bisa berhenti di sini.
Implementasi K-Means menggunakan Python:
Sekarang, kita akan mengimplementasikan algoritma K-means dengan python. Untuk mengimplementasikan K-means, kita akan menggunakan dataset Iris yang terkenal, yaitu open-source. Dataset ini memiliki tiga kelas yang berbeda. Dataset ini pada dasarnya memiliki empat fitur: Panjang kelopak, lebar kelopak, panjang kelopak, dan lebar kelopak. Kolom terakhir akan memberi tahu nama kelas dari baris itu seperti setosa.
Datasetnya seperti di bawah ini:
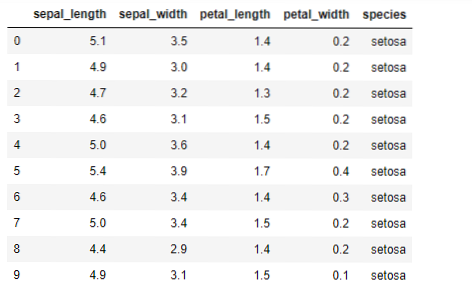
Untuk implementasi python k-means, kita perlu mengimpor perpustakaan yang diperlukan. Jadi kami mengimpor Pandas, Numpy, Matplotlib, dan juga KMeans dari sklearn.cluster seperti yang diberikan di bawah ini:

Kami sedang membaca Iris.csv dataset menggunakan metode read_csv panda dan akan menampilkan 10 hasil teratas menggunakan metode head.
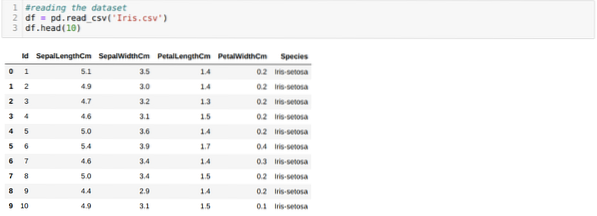
Sekarang, kami hanya membaca fitur-fitur dari kumpulan data yang kami perlukan untuk melatih model. Jadi kita membaca keempat fitur dari dataset (panjang sepal, lebar sepal, panjang petal, lebar petal). Untuk itu, kami meneruskan empat nilai indeks [0, 1, 2, 3] ke dalam fungsi iloc dari bingkai data panda (df) seperti yang ditunjukkan di bawah ini:
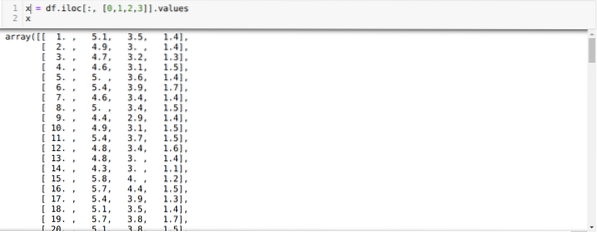
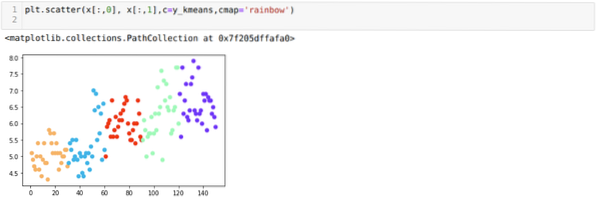
Sekarang, kami memilih jumlah cluster secara acak (K=5). Kami membuat objek kelas K-means dan kemudian memasukkan dataset x kami ke dalamnya untuk pelatihan dan prediksi seperti yang ditunjukkan di bawah ini:
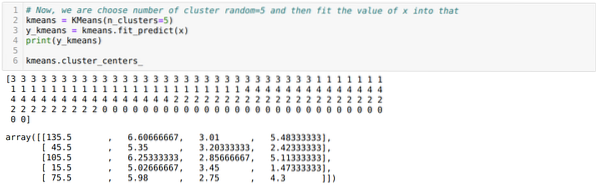
Sekarang, kita akan memvisualisasikan model kita dengan nilai K=5 acak. Kami dapat dengan jelas melihat lima cluster, tetapi sepertinya tidak akurat, seperti yang ditunjukkan di bawah ini.
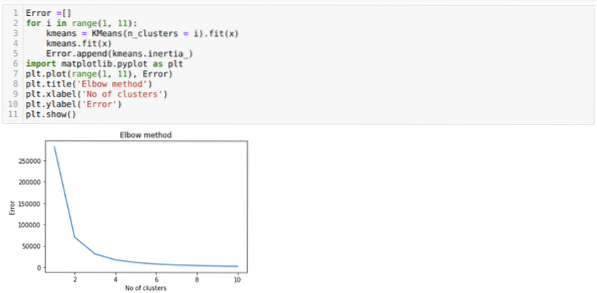
Jadi, langkah kita selanjutnya adalah mencari tahu apakah jumlah cluster itu akurat atau tidak. Dan untuk itu, kami menggunakan metode Elbow. Metode Elbow digunakan untuk mengetahui jumlah cluster yang optimal untuk dataset tertentu. Metode ini akan digunakan untuk mengetahui apakah nilai k=5 benar atau tidak karena kita tidak mendapatkan clustering yang jelas. Jadi setelah itu, kita menuju ke grafik berikut, yang menunjukkan nilai K=5 tidak benar karena nilai optimal berada di antara 3 atau 4.
Sekarang, kita akan menjalankan kembali kode di atas dengan jumlah cluster K=4 seperti gambar di bawah ini:
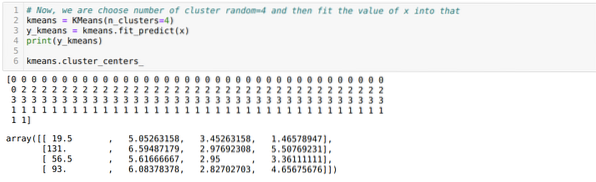
Sekarang, kita akan memvisualisasikan pengelompokan build baru K=4 di atas. Layar di bawah ini menunjukkan bahwa sekarang pengelompokan dilakukan melalui k-means.
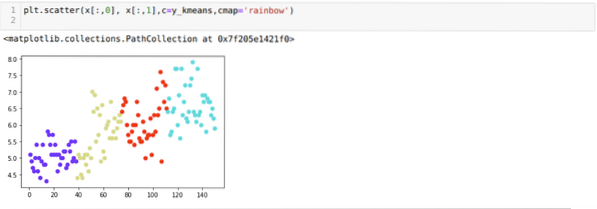
Kesimpulan
Jadi, kami mempelajari algoritma K-means dalam kode numerik dan python. Kami juga telah melihat bagaimana kami dapat mengetahui jumlah cluster untuk kumpulan data tertentu. Terkadang metode Elbow tidak dapat memberikan jumlah cluster yang benar, sehingga dalam hal ini ada beberapa metode yang dapat kita pilih.
 Phenquestions
Phenquestions